从直线绘制箭头

算法分析¶

给定起点和终点，想绘制一个有厚度的箭头，如下：

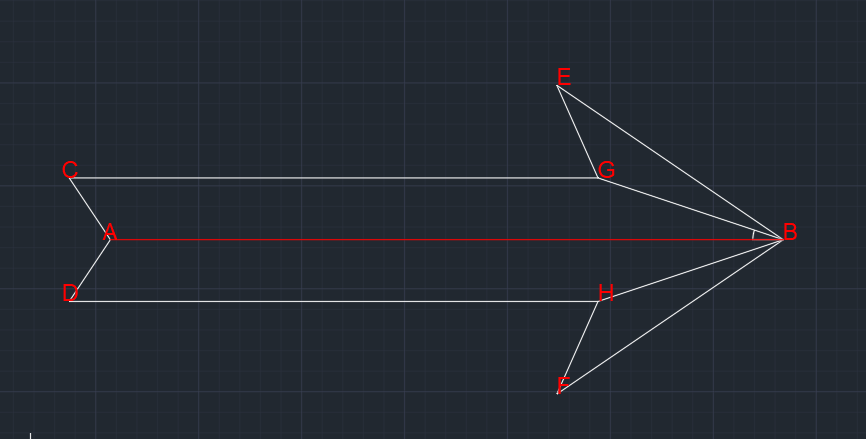
已知A、B两点的坐标，以AB作为中心线，绘制出一条有厚度的箭头，白色的箭头为想要的效果。

其实这个就是要求C、D、E、F、G、H这些点的坐标，求出来之后，如何练成线都可以。把需求拆分成数学问题，然后把数学问题抛给Kimi，让Kimi生成数学算法。

提示词¶

已知A、B点的坐标，求：
1. 求与AB向量形成124度夹角的向量AC，AD，其中AB向量逆时针转124度到AC向量，AB向量顺时针转124度转到AD向量，已知AC=AD=1000,求C、D点的坐标，
2. 求与BA向量形成34度夹角的向量BE，BF，其中BA向量逆时针转34度到BF向量，BA向量顺时针转34度转到BE向量，已知BE=BF=3000,求E、F点的坐标，


要求：用C#代码实现，并且封装成两个方法，

方法1：传入A、B两点的坐标、124度夹角,以及AC、AD的长度，AC、AD长度相等，传一个参数即可，4个已知条件作为参数传入，返回C、D两点的坐标，
方法2：传入A、B两点的坐标、34度夹角，以及BE、BF的长度，BE、BF长度相等，传一个参数即可4个已知条件作为参数传入，返回E、F两点的坐标，

通用条件：   

    1. 点类用Point3d表示，假设点类已经有X、Y、Z三个属性，支持基本运算，不用展示Point3d的实现代码，只需要展示封装的算法的代码。
    2. 不用展示测试代码

结果¶

以下是用C#实现的两个方法的代码，分别用于求解问题中的C、D点坐标和E、F点坐标。代码中使用了向量旋转公式来计算目标点的坐标。

using System;
using System.Numerics;

public class Point3d
{
    public double X { get; set; }
    public double Y { get; set; }
    public double Z { get; set; }

    public Point3d(double x, double y, double z)
    {
        X = x;
        Y = y;
        Z = z;
    }
}

public class VectorUtils
{
    // 方法1：计算C、D点坐标
    public static (Point3d C, Point3d D) CalculateCD(Point3d A, Point3d B, double angle124, double lengthACAD)
    {
        // 计算AB向量
        double abX = B.X - A.X;
        double abY = B.Y - A.Y;

        // 将角度转换为弧度
        double angleRad = angle124 * Math.PI / 180.0;

        // 逆时针旋转124度得到AC向量
        double acX = abX * Math.Cos(angleRad) - abY * Math.Sin(angleRad);
        double acY = abX * Math.Sin(angleRad) + abY * Math.Cos(angleRad);

        // 顺时针旋转124度得到AD向量
        double adX = abX * Math.Cos(-angleRad) - abY * Math.Sin(-angleRad);
        double adY = abX * Math.Sin(-angleRad) + abY * Math.Cos(-angleRad);

        // 计算C、D点坐标
        Point3d C = new Point3d(A.X + acX * lengthACAD / Math.Sqrt(abX * abX + abY * abY),
                                A.Y + acY * lengthACAD / Math.Sqrt(abX * abX + abY * abY),
                                A.Z);
        Point3d D = new Point3d(A.X + adX * lengthACAD / Math.Sqrt(abX * abX + abY * abY),
                                A.Y + adY * lengthACAD / Math.Sqrt(abX * abX + abY * abY),
                                A.Z);

        return (C, D);
    }

    // 方法2：计算E、F点坐标
    public static (Point3d E, Point3d F) CalculateEF(Point3d A, Point3d B, double angle34, double lengthBEF)
    {
        // 计算BA向量
        double baX = A.X - B.X;
        double baY = A.Y - B.Y;

        // 将角度转换为弧度
        double angleRad = angle34 * Math.PI / 180.0;

        // 逆时针旋转34度得到BF向量
        double bfX = baX * Math.Cos(angleRad) - baY * Math.Sin(angleRad);
        double bfY = baX * Math.Sin(angleRad) + baY * Math.Cos(angleRad);

        // 顺时针旋转34度得到BE向量
        double beX = baX * Math.Cos(-angleRad) - baY * Math.Sin(-angleRad);
        double beY = baX * Math.Sin(-angleRad) + baY * Math.Cos(-angleRad);

        // 计算E、F点坐标
        Point3d E = new Point3d(B.X + beX * lengthBEF / Math.Sqrt(baX * baX + baY * baY),
                                B.Y + beY * lengthBEF / Math.Sqrt(baX * baX + baY * baY),
                                B.Z);
        Point3d F = new Point3d(B.X + bfX * lengthBEF / Math.Sqrt(baX * baX + baY * baY),
                                B.Y + bfY * lengthBEF / Math.Sqrt(baX * baX + baY * baY),
                                B.Z);

        return (E, F);
    }
}

代码说明¶

向量旋转公式：
逆时针旋转公式：
[ \begin{cases} x' = x \cdot \cos(\theta) - y \cdot \sin(\theta) \ y' = x \cdot \sin(\theta) + y \cdot \cos(\theta) \end{cases} ]
顺时针旋转公式：
[ \begin{cases} x' = x \cdot \cos(-\theta) - y \cdot \sin(-\theta) \ y' = x \cdot \sin(-\theta) + y \cdot \cos(-\theta) \end{cases} ]
计算目标点坐标：
首先计算向量的单位向量，然后乘以目标长度，最后加上起点坐标。
封装方法：
方法1 CalculateCD 计算C、D点坐标。
方法2 CalculateEF 计算E、F点坐标。
通用条件：
点类 Point3d 已经定义，支持基本运算，代码中直接使用其属性 X、Y、Z。

这样，通过传入相应的参数，即可计算出目标点的坐标。

展示¶

调用上面Kimi写出的算法，然后自己组合一下，生成箭头的代码如下：

var line = new Line(startPoint, nextPoint);
// 绘制箭头预览
var (pC, pD) = CalculateCD(startPoint, nextPoint, 124, 1000);
var (pE, pF) = CalculateEF(startPoint, nextPoint, 34, 3000);
var (pG, pH) = CalculateEF(startPoint, nextPoint, 18, 2300);
var arrowPoints = new List<Point3d>()
{
    startPoint,pC,pG,pE,nextPoint,pF,pH,pD,startPoint
};
for (int i = 0; i < arrowPoints.Count - 1; i++)
{
    var l = new Line(arrowPoints[i], arrowPoints[i + 1]);
    queue.Enqueue(l);
}

结果展示：

从直线绘制箭头

算法分析¶

提示词¶

结果¶

代码说明¶

展示¶

评论